Question

Suppose that IQ scores have a a bell shaped distribution with a mean of 96 and the standard deviation of 17. Using the empirical rule what percentage of IQ scores are no more than 79 please do not round your answer

Answer 1

GIVEN:

We are given that IQ scores have a bell shaped distribution with a mean of 96 and a standard deviation of 17.

Required;

Using the emperical rule, what percentage of IQ scores are no more than 79?

Step-by-step explanation;

For a bell-shaped distribution, we already know that,

68% of the data set lies within one standard deviation

95% of the data set lies within two standard deviations

99.7% of the data set lies within three standard deviations

The condition given is that the IQ scores are no more than 79, hence;

`\begin{gathered} n=(79-96)/(17) \\ \\ n=(-17)/(17)=-1 \end{gathered}`

Now we can see that the IQ score of 79 is 1 standard deviation to the left of the mean (that is to the left of 96).

We also take note that 68% of the data set lies within one standard deviation on either side of the mean.

Therefore, for the IQ scores to be 1 standard deviation from the mean, we would have;

`\begin{gathered} (1-68\%)/(2)=(1-0.68)/(2) \\ \\ =0.16 \end{gathered}`

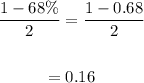
Expressed as a percentage, we now have

`1.6\%`

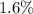
ANSWER:

Therefore, 1.6% of IQ scores would be no more than 79.