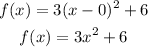Question

A quadratic function in vertex form whose graph has a vertex of (0,6) and passes through the point (-1,9)

Answer 1

`\begin{gathered} h=0 \\ k=6 \\ x=1 \\ y=9 \end{gathered}`

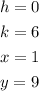
the vertex form of the equation can be written as;

`f(x)=3(x-0)^2+6`

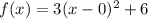
The standard form of the quadratic equation is;

`f(x)=3x^2+6`

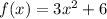
Step-by-step explanation:

Given that the vertex is (0,6);

`\begin{gathered} (h,k)=(0,6) \\ h=0 \\ k=6 \end{gathered}`

And passes through the point (-1,9);

`\begin{gathered} (x,y)=(1,9) \\ x=1 \\ y=9 \end{gathered}`

Recall that the vertex form of a quadratic equation can be written as;

`y=a(x-h)^2+k`

To get the value of a, let us substitute the given values;

`\begin{gathered} y=a\mleft(x-h\mright)^2+k \\ 9=a\mleft(1-0\mright)^2+6 \\ 9=a+6 \\ 9-6=a \\ a=3 \end{gathered}`

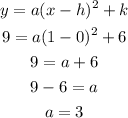
Therefore, the vertex form of the equation can be written as;

`\begin{gathered} f(x)=a(x-h)^2+k \\ f(x)=3(x-0)^2+6 \end{gathered}`

The standard form of the quadratic equation is;

`\begin{gathered} f(x)=3(x-0)^2+6 \\ f(x)=3x^2+6 \end{gathered}`