Question

What is the ratio of thicknesses of polystyrene and flint glass that would contain the same number of wavelengths of light? (Use any necessary data found in this table.)tpolystyrene/flint glass =

Answer 1

Let's find the ratio of thickness of polystyrene and flint glass that would contain the same number of wavelengths of light.

The relation of wavelength for any given medium is:

`\lambda_n=(\lambda)/(n)`

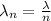
Where:

λn is the wavelength of the wave medium.

λ is the wavelength in vacuum.

n is the refractive index of the medium.

Now, for the thickness, we have:

`{(d_p)/(\lambda_p)}=(d_f)/(\lambda_f)`

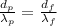
dp is the thickness of of polystyrene

df is the thickness of flint glass.

λp is the wavelength of light in polystyrene.

λf is the wavelength of light in flint glass.

Substitute λ/np for λp and λ/nf for λf:

`\begin{gathered} (d_p)/((\lambda)/(n_p))=(d_f)/((\lambda)/(n_f)) \\ \\ (d_p)/(d_f)=((\lambda)/(n_p))/((\lambda)/(n_f)) \\ \\ (d_p)/(d_f)=(n_f)/(n_p) \end{gathered}`

Where:

nf is the refractive index of flint glass = 1.66

n is the refractive index of polystyrene = 1.49

Thus, we have:

`\begin{gathered} (d_p)/(d_f)=(1.66)/(1.49) \\ \\ (d_p)/(d_f)=1.114 \end{gathered}`

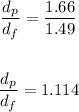
Therefore the ratio of thicknesses of polystyrene and flint glass that would contain the same number of wavelengths of light is 1.114

ANSWER:

1.114