Question

Felipe borrowed $8000 at a rate of 16.5%, compounded monthly. Assuming he makes no payments, how much will he owe after 7 years? Round your answer to the nearest cent

Answer 1

$25,193.17

Explanation:

Given:

• Principal Felipe borrowed, P=$8000

,

• Annual Interest Rate, r=16.5%=0.165

,

• Compounding Period, k=12 (Monthly)

,

• Time, t=7 years

We want to determine how much he will owe after 7 years.

In order to carry out this calculation, use the compound interest formula below:

`A(t)=P\mleft(1+(r)/(k)\mright)^(tk)`

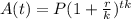
Substitute the values defined above:

`A(t)=8000\mleft(1+(0.165)/(12)\mright)^(12*7)`

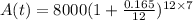
Finally, simplify and round to the nearest cent.

`\begin{gathered} A(t)=8000(1+0.01375)^(84) \\ =8000(1.01375)^(84) \\ =\$25,193.17 \end{gathered}`

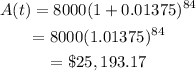
After 7 years, Felipe will owe $25,193.17.