Solution:
Given:
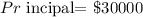
Let x be the principal for the 8% simple interest per year
Let y be the principal for the 6% simple interest per year
Hence,

The formula for calculating simple interest is;
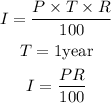
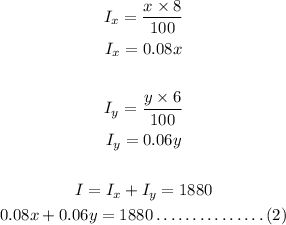
Solving the two equations simultaneously;

Therefore,
Lucy invested $4,000 principal for 8% simple interest.
Lucy invested $26,000 principal for 6% simple interest.