Question

A rock that is dropped from the top of a cliff reaches the ground moving with a speed of 50 m/s. How high is the cliff?

Answer 1

Since the rock is dropped from the top this is a free fall motion. This means that the initial velocity is zero and that we can use the following formulas:

`g=(v_f-v_0)/(t)`
`y=y_0+v_0t+(1)/(2)gt^2`
`v^2_f-v^2_0=2g(y-y_0)`

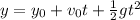
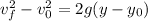
Now, before we can use this formulas we have to do two things:

0. We have to determine what ,we need to find and what we have,. In this case we need to find the height of the cliff, this means that we need to find the change in position of the rock; and we have the initial velocity, the gravitational acceleration and the final velocity (the final speed). ,Hence we can use the third equation,.

,

1. We need to determine which direction is positive and where is the origin of motion. Since the motion is downward we are going to establish that down in the positive direction of motion; and since we dropped the rock from the top os the cliff this will be our origin of motion. With this in mind we have that g=10 m/s^2, vf=50 m/s and that y0=0.

With this in mind we have that:

`\begin{gathered} (50)^2-(0)^2=2(10)(y-0) \\ 2500=20y \\ y=(2500)/(20) \\ y=125 \end{gathered}`

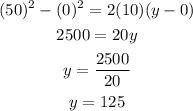
Therefore the cliff is 125 meters high.