Question

Can someone please explain it to me I don't get it

Answer 1

We have the general rule for a rotation of 90° counterclockwise:

`r_(90)(x,y)=(y,-x)`

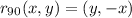
and the general rule for a y=-x reflection is:

`r_(y=-x)(x,y)=(-y,-x)`

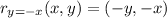
In this case, we have the points R=(2,-2), S=(5,-1) and T=(3,-5).

Then, we first have to use the 90° rotation on all points:

`\begin{gathered} r_(90)(R)=r_(90)(2,-2)=(-2,-2)=R^(\prime) \\ r_(90)(S)=r_(90)(5,-1)=(-1,-5)=S^(\prime) \\ r_(90)(T)=r_(90)(3,-5)=(-5,-3)=T^(\prime) \end{gathered}`

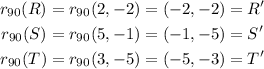
Now we use the y=-x reflection on our new points:

`\begin{gathered} r_(y=-x)(R^(\prime))=r_(y=-x)(-2,-2)=(2,2)=R^(\doubleprime) \\ r_(y=-x)(S^(\prime))=r_(y=-x)(-1,-5)=(5,1)=S^(\doubleprime) \\ r_(y=-x)(T^(\prime))=r_(y=-x)(-5,-3)=(3,5)=T^(\doubleprime) \end{gathered}`

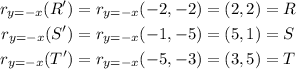
therefore, the final points after the transformations are:

R''=(2,2)

S''=(5,1)

T''=(3,5)