Question

For what value(s) of p will the quadratic equation x^2+x+(p+7)=0 have equal roots?

Answer 1

Given:

`x^2+x+(p+7)=0`

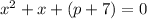
Let's find the value(s) of p where the equation will have equal roots.

To find the value of p, apply the quadratic formula:

`p=(-b\pm√(b^2-4ac))/(2a)`

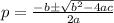
When there are equal roots, the discriminant is zero.

Thus, we have:

`D=b^2-4ac=0`

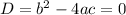
Where:

a = 1

b = 1

c = (p + 7)

Thus, we have:

`\begin{gathered} 1^2-4(1)(p+7)=0 \\ \\ 1^2-4p-4(7)=0 \\ \\ 1^2-4p-28=0 \\ \\ -4p-28+1=0 \\ \\ -4p-27=0 \end{gathered}`

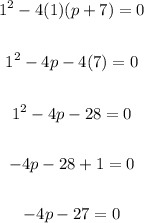
Now, let's solve for p.

Add 27 to both sides:

`\begin{gathered} -4p-27+27=0+27 \\ \\ -4p=27 \\ \\ \text{ Divide both sides by -4:} \\ (-4p)/(-4)=(27)/(-4) \\ \\ p=-(27)/(4) \end{gathered}`

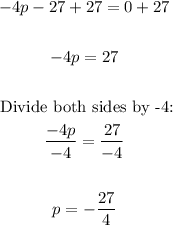
Therefore, the value of p where the equation will have equal roots are:

`-(27)/(4)`

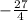
ANSWER:

`p=-(27)/(4)`