Question

4. Solve the equation using square roots.x2 + 10 = 9x^2+10x=9

Answer 1

Given:

The area of the playground is 204 square yd.

The width of the playground is 5 yd longer than its length.

Let, w be the with of the playground and l is length.

`w=5+l`

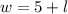
The area is given as,

`\begin{gathered} A=l* w \\ 204=l*(l+5) \\ l^2+5l-204=0 \\ Use\text{ quadratic formula:} \\ l=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a},a=1,b=5,c=-204 \\ l=\frac{-5\pm\sqrt[]{5^2-4*1*(-204)}}{2} \\ l=(-5\pm\: 29)/(2) \\ l=(-5+29)/(2),l=(-5-29)/(2) \\ l=12,l=-17 \end{gathered}`

As length can not be negative.

Hence, length = l =12 yd

Width = w = l +5 = 12+5 =17 yd.

Answer: owidth is 17 yds.