Question

Brayden is saving money to buy a new bike after 2 weeks he saved one $80 after 4 weeks he saved $260 write an equation that can be used to model the number of dollars y Braden saves over ex weeks explain what the slope and y-intercept of your equation mean in this context

Answer 1

Step1:

The formula for finding the slope is given below:

`\text{Slope =}(y_2-y_1)/(x_2-x_1)`
`\begin{gathered} \text{Where x}_1=2weeks;y_1=\text{ \$80} \\ x_{2_{}}=4\text{ we}eks;y_2=\text{ \$260} \end{gathered}`

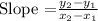
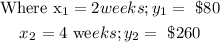
Substituting these values into the formula above, we get

`\text{Slope =}(260-80)/(4-2)=(180)/(2)=90`

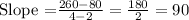
Step2:

The required equation model can be obtained with the formula below:

`\begin{gathered} y-y_1=slope(x-x_1) \\ \text{Where x}_1=2;y_1=\text{ 80} \\ \text{Now, substituting these values into the formula, we get} \\ y-80=90(x-2) \end{gathered}`
`\begin{gathered} \text{Clearing the brackets, we get} \\ y-80=90x-180 \\ \text{Collecting the like terms, we get} \\ y=90x-180+80 \\ y=90x-100 \end{gathered}`

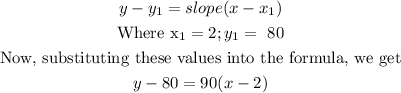
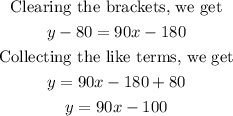
The correct equation model is y = 90x -100.

The slope is 90. This implies that for every Brayden saves $90.

The y-intercept is -100. This means that there is a fixed deduction of $100 from whatever amount that Brayden saved to buy the new bike.