Given data:
* The radius of the circular motion of the car is r = 48.2 m.
* The acceleration of the car is,
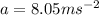
Solution:
The centripetal force acting on the car in terms of the acceleration is,
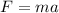
The centripetal force acting on the car in terms of velocity and radius is,
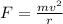
As the force acting on the car is the same in either case, thus,
![\begin{gathered} (mv^2)/(r)=ma \\ (v^2)/(r)=a \\ v^2=ra \\ v=\sqrt[]{ra} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/a6hc4ss29d5q1ea3hc1bjdr5pwa0ar9cqn.png)
Substituting the known values,
![\begin{gathered} v=\sqrt[]{48.2*8.05} \\ v=19.7\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/2yh4i871yuigc52n62aqwtk00ztc8fwmfo.png)
Thus, the velocity of the car is 19.7 meters per second.