inConsider the h(x) as the parental function

To determine the function g(x), there were two transformations performed to the parental function.
-First, they added 1 to the x-term, which results on a horizontal translation of one unit to the left
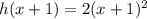
-Second, there were subtracted 8 units to the function, which results in a vertical translation down:
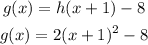
So the function g(x) has the same shape as function h(x) but its vertex is on the coordinates (-1,-8)