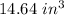Given the box of popcorns and the cone of popcorns, you can assume that the box is a rectangular prism.
You can use this formula to calculate the volume of the box:
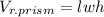
Where "l" is the length, "w" is the width, and "h" is the height.
In this case:
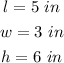
Using the formula, you get:
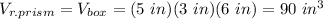
Use this formula to calculate the volume of the cone:
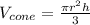
Where "r" is the radius and "h" is the height.
In this case (knowing that the radius is half the diameter):
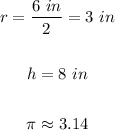
Then, you get:
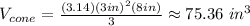
Subtract the volume of the cone from the volume of the box, in order to determine how much more the box holds than the cone:
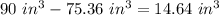
Hence, the answer is: