The polynomila function is,
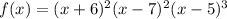
For the zeros of the function f(x) = 0. So,
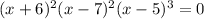
So zeros of the function are x = -6, x = 7 and x = 5.
The multiplicity of zero, x = -6 is two as factor (x + 6) is raised with power of 2. Simillarly, multiplicity of zero, x = 7 is 2 and multiplicity of zero x = 5 is 3.
Answer:
Zero(s) of multiplicity one: None
Zero(s) of multuiplicity two: -6,7
Zero(s) of multipicity three: 5