Question

-Quadratic Equations-The sum of two integers is 42 and their product is 432. Write and solve an equation to find the two integers.

Answer 1

numbersThe first thing to do is to write the exact relations from the question, as follows:

`\begin{gathered} x+y=42 \\ x* y=432 \end{gathered}`

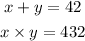
Where X and Y stand for the unknown integer numbers.

Now, we will isolate Y in the first equation and substitute in the second one. This way, we will be able to find the value of X. From this strategy, we perform the calculation that follows:

`\begin{gathered} y=42-x\to x*(42-x)=432 \\ 42x-x^2=432\to0=x^2-42x+432 \\ x^2-42x+432=0 \end{gathered}`

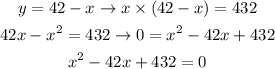
Now, it is important to remember the Bhaskara relation. But first, let's remember that any quadratic equation attends to the following generic form:

`y=ax^2+bx+c`

And we use the Bhaskara relation to find the values of X where Y is 0. In the present question, the constants are the following:

`\begin{gathered} a=1 \\ b=-42 \\ c=432 \end{gathered}`

And the Bhaskara relation is:

`x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Now, we will substitute the values and perform the calculation.

`\begin{gathered} x_(1,2)=\frac{-(-42)\pm\sqrt[]{(-42)^2-4*1*432}}{2*1} \\ x_(1,2)=\frac{-(-42)\pm\sqrt[]{1,764-1,728}}{2}=\frac{42\pm\sqrt[]{36}}{2}=(42\pm6)/(2) \\ x_1=(42+6)/(2)=(48)/(2)=24_{} \\ x_2=(42-6)/(2)=(36)/(2)=18 \end{gathered}`

As you can see, both numbers, 24 and 18, if summed will result in the number 42. For this reason, we found here, not only the value of X but also the value of Y. Because there is no distinction between X and Y, you say that:

The two number which are integers, their sum is 42 and their multiplication is 432 are the numbers 24 and 18.