The given equation is,

Put y=0 in the above equation and solve for x to find the x intercepts.
Putting y =0 in the above equation,
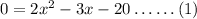
The above equation is in the form of a quadratic equation given by,

Comparing the equations, a=2, b=-3 and c=-20.
Now, using discriminant method solve equation (1) for x.
![\begin{gathered} x=\frac{-(-3)\pm\sqrt[]{(-3)^2-4*2*(-20)}}{2*2} \\ =\frac{3\pm\sqrt[]{9^{}+160}}{4} \\ =\frac{3\pm\sqrt[]{169}}{4} \\ =(3\pm13)/(4) \\ x=(3+13)/(4)\text{ or x=}(3-13)/(4) \\ x=(16)/(4)\text{ or x=}(-10)/(4) \\ x=4\text{ or x=}(-5)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jcujwbot2bj6rjgxtbe1b0jcy45g4zkfj9.png)
Therefore, the x intercepts of the graph of the given equation is x=4 or x=-5/2.