Question

I need help with this assignment that I have no clue how to do.

Answer 1

Let me illustrate the problem first.

We have to get the distance from the catcher to the second base because that is where the catcher needs to throw to tag the runner out at 2nd base. (yellow line)

To solve that, we can use the Pythagorean Theorem.

`c^2=a^2+b^2`

where "a" and "b" are the lengths of the baselines or the legs of the triangle and "c" is the distance from the catcher to the 2nd base or the hypotenuse of the triangle.

In the problem, the legs are both 60ft. Let's plug this in to the formula above.

`c^2=60^2+60^2`

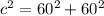
Then, solve for "c".

`\begin{gathered} c^2=3600+3600 \\ c^2=7200 \\ \text{Get the square root of both sides.} \\ \sqrt[]{c^2}=\sqrt[]{7200}^{} \\ c=60\sqrt[]{2}\approx84.85ft \end{gathered}`

Therefore, the distance from the catcher to the 2nd base is 60√2 ft or approximately 84.85 ft.

The catcher needs to throw the ball to the shortstop that is 84.85 ft far to tag the runner out at 2nd base.