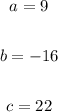Question

Vertices A(a, -6, 2), B(4,b,-9), C(3,5,c) and D(-2,-5,11) form a parallelogram. Determine the values of a,b,c.

Answer 1

Let's do a quick draw to help us visualize the problem:

That's a generic parallelogram, to verify that it's a parallelogram we can see that

`\begin{gathered} AB=CD \\ \\ BC=AD \end{gathered}`

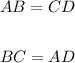
The opposite lengths are equal, then, let's do something similar here, let's say that

`\vec{AB}=\vec{CD}`

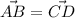
then

`\begin{gathered} \vec{AB}=B-A=(4,b,-9)-(a,-6,2)=(4-a,b+6,-9-2) \\ \\ \vec{AB}=(4-a,b+6,-11) \end{gathered}`

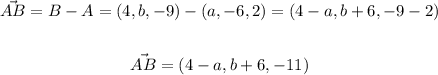
And the vector CD

`\begin{gathered} \vec{CD}=D-C=(-2,-5,11)-(3,5,c)=(-2-3,-5-5,11-c) \\ \\ \vec{CD}=(-5,-10,11-c) \end{gathered}`

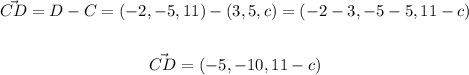
Let's impose our condition

`\begin{gathered} \begin{equation*} \vec{AB}=\vec{CD} \end{equation*} \\ \\ (4-a,b+6,-11)=(-5,-10,11-c) \\ \\ \end{gathered}`

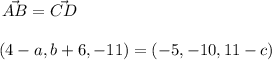
Then

`\begin{gathered} 4-a=-5 \\ \\ b+6=-10 \\ \\ 11-c=-11 \end{gathered}`

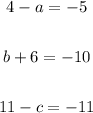
By solving that equations we get

`\begin{gathered} a=9 \\ \\ b=-16 \\ \\ c=22 \end{gathered}`