We are given the vertex of the parabola (0,4) and the directrix y=2. This is a parabola with its axis of symmetry parallel to the y-axis.
The standard form of the parabola is
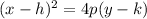
Where (h,k) is the vertex of the parabola and the directrix is given as
y = k - p
We can find the value of p:
p= k - y = 4 - 2 = 2
Substituting, we have the equation of the parabola:
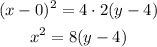
The first choice is correct