Step-by-step explanation
In order to find the standard deviation of the sample we first need to find its mean. The mean of the sample is given by adding all the values of it and then dividing the result by the size of the sample. In this case the size is 6 since we have 6 values so the mean of this sample is:
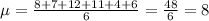
Now that we have found the mean the next step is to find the square deviation of each value. The square deviation of a value x is given by the following formula:
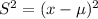
Where μ is the mean of the sample that we found before. Then the square deviations of the six values in the sample are:
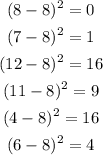
Then we have to find the variance which is the mean of the square deviations i.e. the mean of the six values we just found. The variance is:
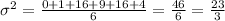
The standard deviation is the square root of the variance so we get:
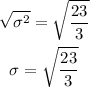
Answer
If we round to two decimal places the answer is 2.77