Let's first draw the scenario to better understand the question.
Equation of segment A = 2x + 1
Equation of segment B = 3x + 4
It also says that the second segment is two times the length of the first segment.
We will use that relationship to find x.
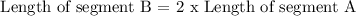

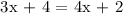
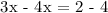
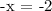
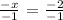
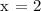
Therefore, x = 2