Answer:
Given that,
The parametric equations x=4t and y=t^2
To find the polar form of the parametric equations
Step-by-step explanation:
we know that,
The polar form of the equation is expressed in terms of r and theta,
The conversion of Cartesian co-ordinate to Polar co-ordinate is given by,
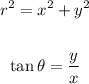
Using this we get,
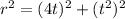
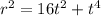

we have that,
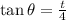
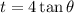
Substitute this we get,

![undefined]()