From the information given, let the speed of the plane in still air be s, and let the speed of the wind be w.
This mean the speed against the wind would be represented by (s - w). Therefore, we would have;
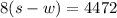
Also, the airplane travels with the wind for the same amount of time, that is 8 hours. This too would be represented by (s + w). We would now have;
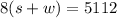
We now have a pair of simultaneous equations which would be solved as follows;

Having calculated w = 40, we now know that the speed of the wind is 40Kmph. We shall now calculate the rate of the plane in still air as follows;
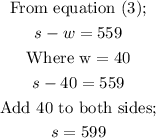
This means the rate of the plane in still air is 599 Kmph.
ANSWER:
Rate of the plane in still air: 599 Kmph
Rate of the