Question

Determine the open intervals where the function is concave upward and the intervals where the function is concave downward. Find the inflection point(s) of the function. F(x)=1/12x^4-2x^2-x+3

Answer 1

The given function is:

`f(x)=(1)/(12)x^4-2x^2-x+3`

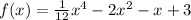
It is required to find the inflection points and determine open intervals where the function is concave upwards and concave downwards.

To do this, find the second derivative of the function and equate it to zero.

Find the first derivative:

`f^(\prime)(x)=(1)/(3)x^3-4x-1`

Differentiate again to get the second derivative:

`f^(\prime\prime)(x)=x^2-4`

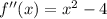
Equate the second derivative to zero and solve for x:

`\begin{gathered} x^2-4=0 \\ \Rightarrow x^2-2^2=0 \\ \Rightarrow(x-2)(x+2)=0 \\ \Rightarrow x=\pm2 \end{gathered}`

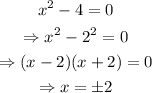
Hence, the inflection points are -2 or +2.

Choose auxiliary points -3,0,3 (on the left of -2, between -2 and +2, and on the right of +2) to test for concavity. If f''(x)>0, then f(x) is concave upward, if f''(x)<0, then f(x) is concave downward.

Substitute x=-2 into the second derivative:

`f^(\prime\prime)(-3)=(-3)^2-4=9-4=5`

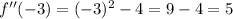
Since f''(-3)>0, it follows that the function is concave upward in the interval (-∞,-2).

Substitute x=0 into the second derivative:

`f^(\prime)^(\prime)(0)=0^2-4=-4`

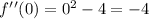
Since f''(0)<0, it follows that the function is concave downward in the interval (-2,2).

Substitute x=3 into the second derivative:

`f^(\prime)^(\prime)(3)=(3)^2-4=9-4=5`

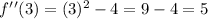
Since f''(3)>0, it follows that the function is concave upward in the interval (2,∞).

Answers:

The inflection points are -2 and +2.

The function is concave upward in the open intervals (-∞,-2) and (2,∞).

The function is concave downward in the open interval (-2,2).