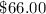Statement Problem: A drama club is planning a bus trip to New York City to see a Broadway play. The cost per person for the bus rental varies inversely to the number of people going on the trip. It will cost $30 per person if 44 people go on the trip. How much will it cost per person if 20 people go on the trip?
Solution:
Let the cost per person for the bus rental be c;
Let the number of people going on the trip be n;
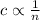
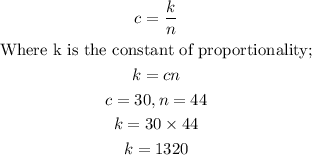
Then, we have;
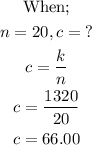
If 20 people go on the trip, the cost per person is;