Question

A circuit with a 21 V battery a 10 Ω resistor and 15 Ω resistor in series. What is the current throughout the circuit?

Answer 1

Given data:

* The voltage across the battery is,

`V=21\text{ volts}`

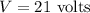
* The value of resistances given is,

`\begin{gathered} R_1=10\text{ ohm} \\ R_2=15\text{ ohm} \end{gathered}`

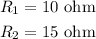
Solution:

The equivalent resistance of the given resistors connected in series is,

`\begin{gathered} R_(eq)=R_1+R_2 \\ R_(eq)=10+15 \\ R_(eq)=25\text{ ohm} \end{gathered}`

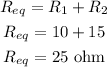
According to Ohm's law, the current through the circuit is,

`\begin{gathered} V=IR_(eq) \\ I=(V)/(R_(eq)) \\ I=(21)/(25) \\ I=0.84\text{ A} \end{gathered}`

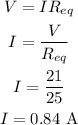
Thus, the current through the circuit is 0.84 A.