Question

Given the function f(x) = (x + 2)/3 determine the slope of the inverse function of f(x) .

Answer 1

First, find the inverse function of f(x). To do so, replace y=f(x) and isolate x from the equation:

`\begin{gathered} f(x)=((x+2))/(3) \\ \Rightarrow y=((x+2))/(3) \\ \Rightarrow3y=x+2 \\ \Rightarrow3y-2=x \\ \therefore x=3y-2 \end{gathered}`

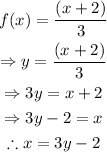
Swap x and y to find the inverse function:

`y=3x-2`

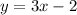
Replace y=f¨-1(x):

`f^(-1)(x)=3x-2`

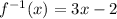
Notice that the inverse function is written in slope-intercept form, and the coefficient of the variable x is the slope. In this case, the coefficient of x is 3.

Therefore, the slope of the inverse function of f(x) is 3.