We need to combine 4 out of 5 girls, and 2 out of 7 boys. The number of ways each of these combinations can be made is:

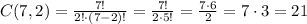
Then, the number of ways both combinations will happen is the product:
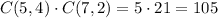
Now, the total number of ways we could choose any 6 students out of 12 (5 girls + 7 boys) is:
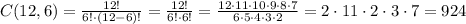
Finally, the required probability is found dividing the number of events of interest (105) by the total number of events (924):
P = 105/924 = 15/132 = 5/44