Given:
In 2000, the population was 6.08 billion
rate of increase = 1.5% per year
Required: The population in 2017
The formula for calculating population growth is:
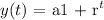
Where y(t) is the population at a later time t
a is the initial population
r is the annual rate of increase
and t is the number of years
For the given problem,
a = 6.08 billion
r = 1.5%
t = 17 years (2017-2000)
Substituting the given values into the formula:

Hence, the population in 2017 should be 7831163611.7