Answer:
A translation of 3 units to the right, followed by a vertical stretch by a factor of 2, followed by a translation of 4 units up.
Explanation:
Transformations


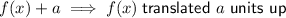
Therefore, the series of transformations of:
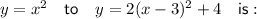
Translated 3 units to the right:
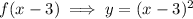
Stretched vertically by a factor of 2:
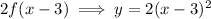
Translated 4 units up:
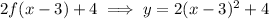
Therefore, the series of transformations is:
A translation of 3 units to the right, followed by a vertical stretch by a factor of 2, followed by a translation of 4 units up.