Question

Robert made a design on his wall with the similar pentagon tiles shown. L R 9 cm 9 cm M K S 15 cm 10 cm 10 cm 15 cm U 10 cm T P 15 cm N * not drawn to scale What is the length of side RS?

Answer 1

RS = 6 cm

Step-by-step explanation:

If the pentagons are similar, the ratio of their sides is constant. So, we can use the following equation to calculate the length of RS:

`(MN)/(ST)=(LM)/(RS)`

Then, we can replace the value of MN by 15 cm, LM by 9 cm, and ST by 10 cm:

`(15)/(10)=(9)/(RS)`

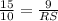
Now, we can solve the equation for RS as:

`\begin{gathered} 1.5=(9)/(RS) \\ 1.5RS=(9)/(RS)\cdot RS \\ 1.5RS=9_{} \\ (1.5RS)/(1.5)=(9)/(1.5) \\ RS=6 \end{gathered}`

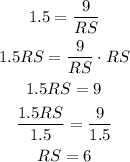
Therefore, the length of the side RS is 6 cm