Question

An angle a in standard position has a terminal side which passes through the point (-5,8)

Answer 1

STEP - BY - STEP EXPLANATION

What to find?

• sin(α)

,

• cos(α)

,

• tan(α)

,

• cot(α)

,

• sec(α)

,

• csc(α)

GIVEN:

Step 1

Make a sketch.

Step 2

Determine the hypotenuse side.

Using the Pythagoras theorem;

`hypotenuse^2=adjacent^2+opposite^2`
`\begin{gathered} hypotenuse=√(5^2+8^2) \\ \\ =√(25+64) \\ \\ =√(89) \end{gathered}`

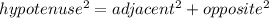
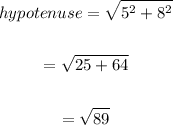
Step 3

Determine the identities.

We know that;

opposite =8

adjacent=5

hypotenuse = √89

`\begin{gathered} sin(\alpha)=(opposite)/(hypotenuse) \\ \\ =(8)/(√(89)) \\ \\ =(8√(89))/(89) \end{gathered}`

Since sine is positive in the second quadrant, then we leave the answer as it is.

Hence;

`sin(\alpha)=(8√(89))/(89)`

`\begin{gathered} cos(\alpha)=(adjacent)/(hypotenuse) \\ \\ =(5)/(√(89)) \\ \\ =(5√(89))/(89) \end{gathered}`

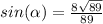
In quadrant II, cos is negative.

Hence;

`cos(\alpha)=-(5√(89))/(89)`

`\begin{gathered} tan(\alpha)=(opposite)/(adjacent) \\ \\ =(8)/(5) \end{gathered}`

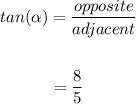
Tangent is negative in quadrant II.

Hence;

`tan(\alpha)=-(8)/(5)`

`\begin{gathered} cot(\alpha)=(1)/(tan\alpha) \\ \\ =(1)/(-(8)/(5)) \\ \\ =-(5)/(8) \end{gathered}`

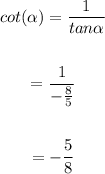
Hence,

`cot(\alpha)=-(5)/(8)`

`\begin{gathered} sec(\alpha)=(1)/(cos(\alpha)) \\ \\ =(1)/(-(5)/(√(89))) \\ \\ =-(√(89))/(5) \end{gathered}`

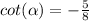
Hence;

`sec(\alpha)=-(√(89))/(5)`

`\begin{gathered} csc(\alpha)=(1)/(sin(\alpha)) \\ \\ =(1)/((8)/(√(89))) \\ \\ =(√(89))/(8) \end{gathered}`

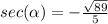
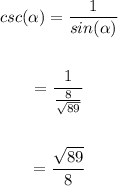
Hence;

`csc(\alpha)=(√(89))/(8)`

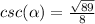
ANSWER

• sin(α) = 8√89 /89

• cos(α) = -5√89 /89

• tan(α)= - 8/5

• cot(α)= -5/8

• sec(α) = - √89 / 5

• cosec(α) =