Given:
Bill is playing a game in which he spins a spinner with 6 equal-sized slices numbered 1 thru 6. The spinner stops on a number slice at random. This game is this: Bill spins the spinner once. He wins $1 if the spinner stops on the number2, $4 if the spinner stops on the number 2, $7 if the spinner stops on the number3, and$10
Required:
To calculate probability
Step-by-step explanation:
(a)
first we want to find the expected value in one spin:
number 1 : wins $1
number 2: wins $4
number 3 : wins $7
number4 : wins $10
number5: looses $11
number 6 : looses $11
The expected value can be calculated as:
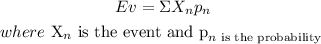
We know that the probability for all the events is 1/6 so we have:
Ev =($1+$4+$7+$10-$11-$11)*(1/6)
=$0
So the expected value for the game is $0
(b) Bill neither gain money nor looses
Required answer:
(a) $0
(b) option C