Question

Hello im doing some practice questions and would like some help. ty

Answer 1

Step-by-step explanation

We can find the area of the rectangle and then subtract the area of the semicircle.

`A=A1-A2`

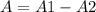
Finding the area of the rectangle

The formula to find the area of a rectangle is:

`A_(rectangle)=\text{ length * width}`

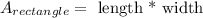
Then, we have:

`\begin{gathered} A1=34in*22in \\ A1=748in^2 \end{gathered}`

Finding the area of the semicircle

The formula to find the area of a semicircle is:

`\begin{gathered} A_{\text{ semicircle}}=(\pi r^2)/(2) \\ \text{ Where } \\ r\text{ is the radius of the circle} \end{gathered}`

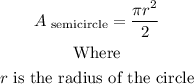
The radius is half of the circle. Then, the radius of the circle is 11 in.

`\begin{gathered} \text{ radius }=\frac{\text{ diameter}}{2} \\ \text{rad}\imaginaryI\text{us}=(22in)/(2) \\ \text{rad}\imaginaryI\text{us}=11in \end{gathered}`

Then, the area of the semicircle is:

`\begin{gathered} A2=(\pi r^(2))/(2) \\ A2=(\pi(11in)^2)/(2) \\ A2=(121\pi\imaginaryI n^2)/(2) \\ A2=60.5\pi\imaginaryI n^2 \end{gathered}`

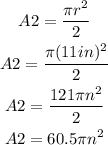
Calculating the area of the paperboard that remains

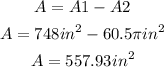
`\begin{gathered} A=A1-A2 \\ A=748in^2-60.5\pi in^2 \\ A=557.93in^2 \end{gathered}`Answer

The area of the paperboard that remains rounding to the nearest hundredth is 557.93 in².