Question

A teacher reaches into a bag that contains 6 plums, 14 clementine's, and 12nectarines. What is the probability that the teacher does not pick a nectarines? Youranswer can be a simplified fraction or rounded to the nearest whole percent.

Answer 1

`{\textcolor{red}{P(NOT\: nectarine)}}=(5)/(8)`

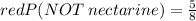
1) Given that the sum of all probabilities must be equal to 1, and there are 6 plums, 14 clementines, and 12 nectarines we can tell there are 14+12+6 objects:

14+12+6= 32 this is our subspace.

2) So let's find first the probability of that teacher picking a nectarine:

`{\textcolor{orange}{P(nectarine)}}=(12)/(32)`

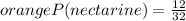
But notice, we don't want to know that we want the probability of not picking a nectarine so let's subtract that from 1 and write it this way:

3) We want to find the probability of the Complementary set to that:

`\begin{gathered} {\textcolor{red}{P(NOT\: nectarine)}}=1-(12)/(32) \\ {\textcolor{red}{P(NOT\: nectarine)}}=(32)/(32)-(12)/(32) \\ {\textcolor{red}{P(NOTnectarine)}}=(20)/(32)=(5)/(8) \end{gathered}`

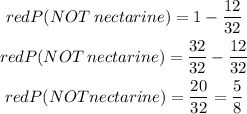
Note that we simplified this.