We can use the law of ideal gases to solve this question.
The law of ideal gases is represented by the following formula:
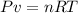
Where P is the pressure, v is the volume, n is the number of moles, R is the ideal gas constant and T is the temperature.
The first step is to convert kPa to atm, °C to K and mL to L.
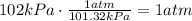
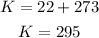
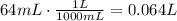
Now, we can use these values to find n, which is the amount of moles of the gas:
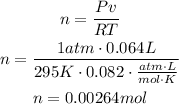
The answer is 0.00264 moles of chlorine are released.