Given data:
* The height of the bullet is 22 m.
* The speed of bullet in the horizontal direction is 524 m/s.
Solution:
By the kinematics equation, the time taken by the bullet to reach the ground is,
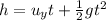
where u_y is the vertical velocity component, t is the time taken to reach the ground, g is the acceleration due to gravity, and h is the height of the bullet,
Substituting the known values,
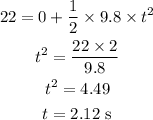
Thus, the time taken by the bullet to reach the ground is 2.12 seconds.
By the kinematics equation for the horizontal motion, the horizontal range of the bullet is,
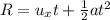
where u_x is the horizontal component of the velocity, a is the acceleration along the horizontal direction, t is the time taken to reach the ground and R is the horizontal range,
Substituting the known values,
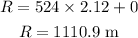
Thus, the horizontal range of the bullet is 1110.9 meters.
Hence, the bullet hit the ground at 1110.9 meters.