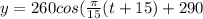Step-by-step explanation
Given
From the question, we can see that the bottom of the ferris wheel is 30 feet about the ground and also while rotating, it can move to a height of 550 feet off the ground. In essence the actual height the ferris wheel can attain is

The amplitude then becomes half of the height which is
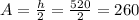
The vertical shift the Ferris wheel undergoes becomes the sum of the amplitude and its distance above the ground.

Since it takes the Ferris wheel 15 minutes to move from bottom to top, it will take it twice that to complete one revolution which will be its period.
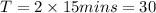
Therefore, the frequency B, becomes;
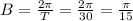
We can then place in the above parameters to form the equation.
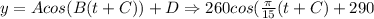
The last missing parameter is the phase shift C. At time t =0, the function (y) has a position at 30. Therefore,
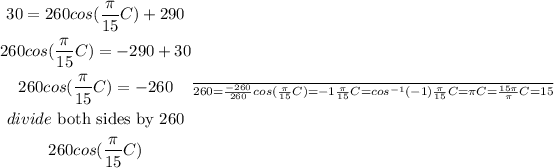
Therefore, the function y becomes
Answer: