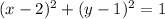Question

A circle is centered at (2, 1) and contains the point (3,-2). Give the equation of the circleWord Bank+3 -2 -1 -1 3.16 10 -2 20 -3 6.32 -1 + 2Blank 1:Blank 2Blank 3.

Answer 1

EXPLANATION

We already know that the equation of the circle centered at (h,k) and that contains the point (x,y) is as follows:

`(x-h)^2+(y-k)^2=r^2`

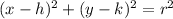
Where h=2 and y=1.

Replacing terms:

`(x-2)^2+(y-1)^2=r^2`

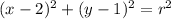
Since (3,-2) is on the graph, we have:

`(3-2)^2+(1-1)^2=r^2`

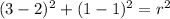
Subtracting numbers:

`1^2+0=r^2\text{ }\longrightarrow\text{ 1=r\textasciicircum{}2}\longrightarrow1=r\text{ }`

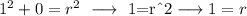
As r=1 our equation is as follows:

`(x-2)^2+(y-1)^2=1`