Question

A raindrop has a mass of 7.7 × 10-7 kg and is falling near the surface of the earth. Calculate the magnitude of the gravitational force exerted (a) on the raindrop by the earth and (b) on the earth by the raindrop.

Answer 1

Given that the mass of the raindrop is

`m=7.7*10^(-7)\text{ kg}`

The acceleration due to gravity is g = 9.81 m/s^2

We have to find

(a) Magnitude of the gravitational force exerted on the raindrop by earth

(b)Magnitude of the gravitational force exerted on the earth by the raindrop

(a) The formula to calculate the magnitude of the gravitational force exerted on the raindrop by the earth is

`F=mg`

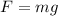
Substituting the values, the gravitational force exerted on the raindrop by the earth is

`\begin{gathered} F=7.7*10^(-7)*9.81 \\ =7.55*10^(-6)\text{ N} \end{gathered}`

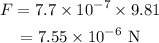
(b) According to Newton's third law,

If F' is the gravitational force exerted on the earth by the raindrop, then

`F=-F^(\prime)`

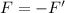
Here, the negative sign indicates that both forces act in opposite direction.

The gravitational force exerted on the earth by the raindrop is

`F^(\prime)\text{ = -7.55}*10^(-6)\text{ N}`

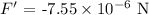
And the magnitude of the gravitational force exerted on the earth by the raindrop is

`7.55*10^(-6)\text{ N}`

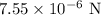
Thus, the magnitude of both forces is equal.