Given data:
* The current through the circuit is,
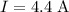
* The value of resistances given is,
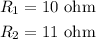
Solution:
The equivalent resistance of the resistors connected in parallel is,
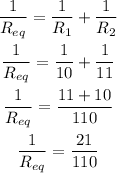
By simplifying,
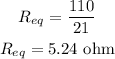
According to Ohm's law, the voltage across the battery in terms of the current and equivalent resistance is,
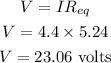
Thus, the voltage across the battery is 23.06 volts.