First, identify a relation between a change in time and a change in distance.
Let Δt be a change in time and Δd be a change in distance.
Since an increase of 3 units in t corresponds to an increase of 8 units in d, then:
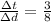
To find a line with that characteristics, set the initial values for time and distance equal to 0, so that Δt = t and Δd =d. Then:
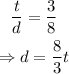
Graph that line by finding two points on it. Notice that when t=0, then d=0 and when t=3, d=8. So, (0,0) and (3,8) belong to that line:
Since we know that Δd=(8/3)Δt, the unit rate of change will be found by plugging in Δt=1:
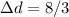
Since Δd is equal to 8/3 when Δt is equal to 1, then the unit rate of change is 8/3.
Therefore, the unit rate of change is 8/3. The graph is shown.