Question

Los Angeles workers have an average commute of 33 minutes. Suppose the LA commute time is normally distributed with a standard deviation of 12 minutes. Let X represent the commute time for a randomly selected LA worker. Round all answers to 4 decimal places where possible.a. What is the distribution of X? X ~ N(b. Find the probability that a randomly selected LA worker has a commute that is longer than 37 minutes. c. Find the 80th percentile for the commute time of LA workers.

Answer 1

We have a normally distributed variable X with mean 33 minutes and standard deviation of 12 minutes.

a. The distribution of X can be expressed as:

`\begin{gathered} \mu=33 \\ \sigma^2=12^2=144 \\ \Rightarrow X\sim N(33,144) \end{gathered}`

b. We can calculate the probability P(X > 37) using the z-score for X = 37 and then looking for the standard normal probability for that z-score.

We can calculate the z-score as:

`\begin{gathered} z=(X-\mu)/(\sigma) \\ z=(37-33)/(12) \\ z=(4)/(12) \\ z=(1)/(3) \end{gathered}`

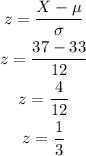
We can now look for the probability as:

`P(X>37)=P(z>(1)/(3))=0.3694`

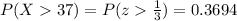
c. The 80th percentile is the value of X for which 80% of the data is below that value.

We can find the z-score that represents the 80th percentile in the standard normal distribution and then convert it to the equivalent value of X in the actual distribution.

Then, we start finding z:

Answer:

a. X ~ N(33, 144)

b. The probability is 0.3694.

c. The 80th percentile is P80 = 43.0994.