We are given three points, and told to find out if they are collinear. What collinear means is that the set of points lay on a line. So, based on this, the strategy to check if this points are collinear is that we are going to pick two points, find the equation of the line that passes through them and them find out if the third point belongs to the line by simply evaluating the equation at the especific value of x.
Let us take, for example the points (-1,11) and (2,23). We will find the line equation that passes through them. To do so, first recall that the line equation is of the form y=mx+b where m is the slope and b is the y-intercept.
First, we will find the slope. Recall that given points (a,b), (c,d) the slope m of the line that joins this two points is given by the equation
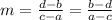
In our case, we take a=-1,b=11, c=2, d=23. Then
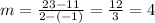
So, so far our equation looks like this

Now, we want the point (-1,11) to belong to this line. That is, that if we replace x by -1, we should also replace y by 11. Then we have
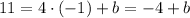
If we add 4 on both sides, we get
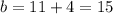
So the equation of the line is

Now, we want to check if (6,42) belongs to this equation. To do so, we replace by 6 and operate. If at the end we get a result of 42, it means that the point belongs to the line, and hence, is collinear to the other two points. We check that
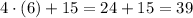
Since we didn't get 42, this means that the point does not belong to the line. Then, the three points are not collinear