Question

The heights of women in college follow a Normal distribution with a mean of 65 inches and a standard deviation of 2.5 inches. Determine the percentage of women with a height between 61 and 68 inches

Answer 1

Let X be the height of women in college. We are told that this variable is distributed as a normal distribution with mean 65 and a standard deviation of 2.5. To solve this problem, we will use a standard normal distribution table. So, the first step is to transform X to a variable Z where Z is a standar normal distribution. We do this by subtracting the mean and dividing by the standard deviation.

Recall that the problem is asking the following probability P(61<=X <= 68).

So, now, lets subtract 65 to the inequality, we get

P(-4<=X-65<=3). Now, we divide everything by the standard deviation, so we get

`P((-4)/(2.5)\le(X-65)/(2.5)\le(3)/(2.5))\text{ =P(}-1.6\le(X-65)/(2.5)\le1.2)`

Now, call Z = (X-65)/2.5. With this transformation Z is distributed now with a standard normal distribution. So the question to answer is

P(-1.6<=Z<=1.2)

This translates to calculating the area under the curve as follows

We can picture two areas

So the area we want to calculate is the sames as the red area minus the blue area. Then, we have the following

`P(-1.6\le Z\le1.2)=P(Z\le1.2)-P(Z\le-1.6)`

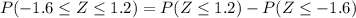
Using a standard deviation table, we have that P(Z<=1.2) = 0.8849 and P(Z<=-1.6) = 0.1446

Then

`P(-1.6\le Z\le1.2)=0.8849-0.1446\text{ = }0.7403`

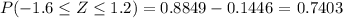
which means that 74.03% of women in college have a height between 61 and 68 inches