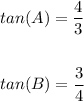Given the triangle ABC, you know that:
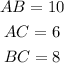
You can identify that the small square in the vertex C of the triangle is a Right Angle (an angle that measures 90 degrees). Therefore, you have to find the tangent of the other two angles:
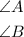
By definition:
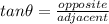
Then:
- For angle A, you can identify that:
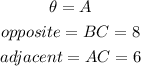
Therefore:

- For angle B:
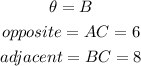
Therefore, you get:
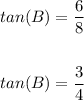
Hence, the answer is: