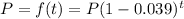
Step-by-step explanation
Step 1
let
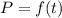
where P represent the population, and t represents the time in years
so,
when t=0, P=2070
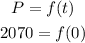
Step 2
if the population decrease 3.9% every year,in decimal form
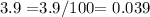
so,after 1 year the population is
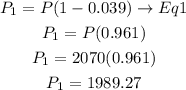
now, after the 2 years
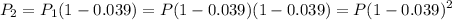
now, after 3 years
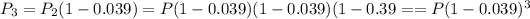
now, we can see the function
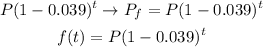
I hope this helps you