Question

In an upstate county in New York state, county administration did a statical study on household electricity bills. The electricity bills are approximately normally distributed with a mean of $200 and a standard deviation of $33. A county clerk selected a random sample 36 electricity bills for this study. What is the probability of getting a sample mean of 36 bills is less than $194? (round to four decimal places) What is the 95th percentile of sampling distribution of mean for samples of 36 bills? (round your answer to a whole number)

Answer 1

We have the electricity bill as a normal random variable with mean $200 and standard deviation $33.

A sample of 36 bills is collected.

The distribution for the sample mean will have the following parameters:

`\begin{gathered} \mu_s=\mu=200 \\ \sigma_s=(\sigma)/(√(n))=(33)/(√(36))=(33)/(6)=5.5 \end{gathered}`

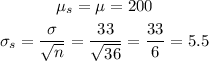
We have to calculate the probability that the sample mean is less than $194.

We will calculate the z-score for X = 194 using the sampling distribution parameters:

`z=(X-\mu_s)/(\sigma_s)=(194-200)/(5.5)=(-6)/(5.5)\approx-1.09091`

We can then use the standard normal distribution table to calculate the probability:

`P(X<194)=P(z<-1.09091)\approx0.1377`

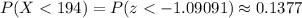
We now have to find the 95th percentile for the sample mean.

This means a value for which 95% of the sample means are below this value.

We can express this as:

Answer:

1) P(X < 194) = 0.1377.

2) X = 209