Question

How do I solve this?Farmer Ed has 1500 meters of fencing, and wants to enclose a rectangular plot that borders on a river. If farmer Ed does not fence the side along the river what is the largest area that can be in enclosed?

Answer 1

We need to find the maximum (Vertex of the function)

Let:

L = Length = 1500 - 2x

W = Width = x

The area is given by:

`\begin{gathered} A=W\cdot L \\ A=x(1500-2x) \\ A=1500x-2x^2 \\ A(x)=1500x-2x^2 \end{gathered}`

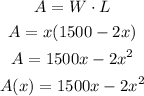
We can find the maximum using the following formula:

`\begin{gathered} xm=-(b)/(2a) \\ where \\ a=-2 \\ b=1500 \\ so\colon \\ xm=-((1500))/(2(-2))=(1500)/(4)=375 \end{gathered}`

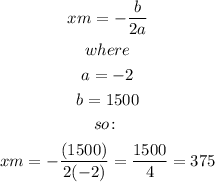
Evaluate the area for the value we found previously:

`A(375)=-2(375)^2+1500(375)=-281250+562500=281250`

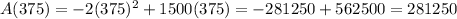
The largest area that can be enclosed is 281250m²