Question

The peak of the extinct volcano Volcán Chimborazo in Ecuador is the farthest point on Earth from Earth's center. This is because Earth bulges outward due to its rotation, and this bulge is greatest at the Equator, which is only about 100 km north of Chimborazo. Volcán Chimborazo's summit is 6,267 m above sea level. If a mountain climber with a mass of 85 kg (climbing equipment included reaches the mountain's peak, what is the gravitational potential energy associated with the climber with respect to sea level?

Answer 1

The gravitational potential enegy associated with the climber is 5.22x10⁶ J.

Given data:

The mass of mountain climber is m=85 kg.

The summit of volcano is h=6267 m.

The expression for the gravitaional potential energy is given by,

`\text{GPE}=\text{mgh}`

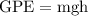
Here, g is the gravitational acceleration whose values is 9.81 m/s².

Substitute the given values in above expression,

`\begin{gathered} \text{GPE}=(85)(9.81)(6267) \\ \text{GPE}=5.22*10^6\text{ J} \end{gathered}`

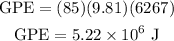
Thus, the gravitational potential enegy associated with the climber is 5.22x10⁶ J.